| |
|
|
|
Radio-Frequency Bridges
Their principles of operation and their relationship to the Wheatstone-Christie prototype.
by David Knight
Introduction:
In this chapter we explore the subject of AC measuring and monitoring bridges; particularly with a view to understanding how they work and how to optimise them for use across the 1.6 - 30MHz HF radio spectrum. In the course of the discussion we will show how to devise bridges that can be used to make accurate measurements of any impedance-related quantity, including reflection-coefficient, impedance magnitude, resistance, conductance, and phase; thereby covering the design considerations for SWR bridges, Match Meters, and bridges for automatic antenna matching systems. Full comprehension of the discussion to follow requires familiarity with the material presented in chapters 1 to 5.
1. Christie's Bridge:
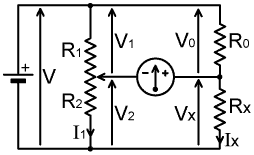
The term 'bridge' came into the language of electrical engineering in connection with the "Wheatstone Bridge", which was actually first described by Samuel Hunter Christie of the Royal Military Academy in Woolwich in 1833. The bridge is usually attributed incorrectly to Sir Charles Wheatstone, who employed it extensively in his scientific experiments, although Wheatstone himself always credited the bridge to Christie [1]. The circuit is so called because the detector (a centre-zero galvanometer, i.e., a microammeter or voltmeter) occupies the position of a bridge between two potential-divider networks. Two possible implementations of Christie's bridge are shown below:
 |
 |
The bridge is balanced by adjusting a variable element until the voltage across the meter (and hence the current through it) is zero. In the left-hand version, the variable element is a potentiometer R1+R2, traditionally constructed by laying a length of resistance wire against a measuring scale, and known as a 'slidewire' [introduced by Kirchhoff. See Gray, Abs Meas E&M 1921, p340]. At balance the ratio R1/R2 is equal to R0/Rx, where R0 is a standard (i.e., a laboratory reference) resistor, and Rx is the unknown resistance under test. In the right-hand version, the ratio R1/R2 is fixed, and R0 is a calibrated variable reference resistor. In this case, it is quite common for R1 to be made equal to R2, because this situation gives greatest meter sensitivity and hence the best accuracy of measurement. When R1=R2, then V1=V2, and the bridge balances when R0=Rx.
There are various ways of proving the balance relationship R1/R2=R0/Rx (see, for example, ref [2]), but here we are interested not so much in measuring resistors, as in generalising the bridge concept and showing that all bridges are direct descendants of Christie's. We will begin therefore by observing that the unknown resistor Rx must obey Ohm's law, i.e.,Vx = IxRx, or:
| Rx = Vx / Ix |
|
Let us observe, for the moment, that we can determine Vx if we need to because we know that, at balance, Vx = V2, and V2 can easily be calculated if we know the supply voltage V and the values of R1 and R2. To determine Ix however, we need to sample the current flowing through the unknown resistor; and we may do this by placing a resistor R0 in series with it, and measuring the voltage V0 that appears across R0. Thus V0 is directly proportional to Ix, i.e., V0=IxR0 and so:
Ix = V0 / R0
If we now substitute this expression for Ix into equation (1.1) above, we obtain:
Rx = R0 Vx / V0
Now at balance, V1=V0 and V2=Vx, and so we can write:
| Rx = R0 V2 / V1 |
Which says that we can determine Rx in comparison to R0 provided that we know the ratio V2/V1. We can easily show that V2/V1=R2/R1 and so write the text-book solution:
Rx = R0 R2 / R1
but the important point is that we do not need to know the supply voltage V, and we do not need to know the absolute values of R1 and R2, only their ratio. Indeed, we do not even need to use resistors R1 and R2, because what we really need is two voltage references V1 and V2, of known ratio; which we might, for example, obtain instead by using two electronically controlled voltage-sources in series.
From the above, we can deduce that a bridge is a device that measures the ratio of two voltages, one being a voltage sample taken from across the device under test, the other being a voltage derived by sampling the current passing through the device under test. Put more formally: a bridge is a device that measures the ratio of a voltage analog and a current analog, an 'analog' being a quantity that is analogous to, i.e., proportional to, the quantity in which we are interested (the British spelling is "analogue"; but the American spelling is nowadays preferable in a technical context, and helps to avoid creating a world shortage of the letters u and e). By comparing two quantities that both vary in proportion to the power-supply voltage, we can make measurements that are independent of the power-supply voltage.
Refs:
[1a] "Wheatstone's Bridge" (J A Fleming) The Encyclopaedia Britannica, 13th Edition 1926. Volume 27.
[1b] "Pioneers of Electrical Communication - Charles Wheatstone IV". Rollo Appleyard, Electrical Communication, Vol. 6, No. 1. July 1927. p2-12.
[1c] The genesis of the Wheatstone bridge. Stig Ekelöf. Engineering sci. & education J. 10 (1), Feb 2001. p37-40.
In the paper in Phil. Trans. Roy. Soc. in which Wheatstone described the DC bridge that now bears his name, he attributes the idea to S.H. Christie. French and German translations published the following year and possibly prepared from a preprint of the paper do not carry this attribution and this might explain why the bridge does not bear Christie's name. This paper discusses the work of both Christie and Wheatstone and why the term 'Wheatstone bridge' and not 'Christie bridge' is used
[2] Advanced Level Physics, M Nelkon and P Parker, 3rd edition (SI) 1974, Heinemann, London. ISBN 0 435 68636 4.
Ch 33: Wheatstone Bridge p829.
2. Arms:
Because of their role in determining the ratio Rx/R0, the voltage splitting resistors R1 and R2, are known as the ratio arms of the bridge. Later on, when we generalise the bridge to AC, we will be able to use devices other than resistors in the voltage splitting network, but they will still be known as the ratio arms. The term "arm" hails from the 19th Century, and seems to have arisen in an ad hoc way for want of terminology to use while explaining bridges (arms are appendages that splay-out from a node). The term has since acquired a life of its own however; and nowadays (according to Langford-Smith [3]), an arm is defined as "a distinct set of elements, electrically isolated from all other conductors except at two points". Hence an arm is a two-terminal network, and the idea that it is one of a series-connected pair is perhaps less essential. On that basis, a bridge has six arms.
Ref:
[3] Radio Designer's Handbook, Ed. Fritz Langford-Smith. 4th edition. 4th impression (with addenda), Iliffe Publ. 1957 [A later reprint exists (1967) ISBN 0 7506 36351]
Arm (Definition), section 4.7.
[Langford-Smith's definition is poor. An arm is one of a series connected pair of two terminal networks in the basic bridge, but multi-terminal networks are also used - eg. transformers]
3. Reciprocity:
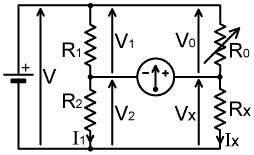
In the diagram below, the positions of the meter and the battery in the bridge discussed earlier have been interchanged.
The swap has made rather a mess of our original voltage and current definitions, and so the circuit is re-drawn on the right to make the analysis more obvious. Using the same arguments as before, we may observe that, at balance, Rx/R2=R0/R1, i.e.:
Rx = R0 R2 / R1
Which is exactly the same result as was obtained previously. This means that the battery and the meter can be swapped without affecting the balance of the bridge; or to put it formally: the bridge is a linear reciprocal network, its measuring function being unaffected by transposition of the generator and the detector. The term 'linear' refers to the fact that the elements within it obey Ohm's law, i.e., the graph of voltage against current is a straight line. If the devices used to make a bridge are non-linear (e.g., semiconductor diodes) then the bridge is not a reciprocal network.
4. Generalising the Bridge:
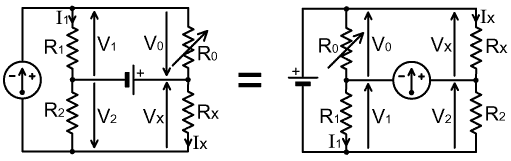
We may just as well use Christie's bridge by replacing the battery with an AC generator and the galvanometer with a detector sensitive to alternating voltages. Analysis of the bridge however then entails treating all of the voltages and currents involved as phasors; but (as always) we can satisfy this requirement by writing impedances as complex numbers and deriving expressions for the voltages and currents from them. Here we will use the notation and various simplifying techniques developed in chapter 1. In particular, quantities that must be treated as vectors will be written in bold; and we are at liberty to nominate one vector in any complete set to be a reference vector, and by choosing its direction to be 0°, may treat it and any other vectors in phase with it as scalars (i.e., real numbers) [AC Theory, 24.5].
| The AC version of the
bridge, with attendant vectors is shown on the right. In order to
analyse this network, we first observe that V1+V2 must be equal to V0+Vx, and that the voltage across the
detector D (Vdet)
is equal to both V1-V0 and Vx-V2, i.e., V0 + Vx = V1 + V2 Vdet = V1 - V0 Vdet = Vx - V2 |
 |
Let us assume, for the time
being, that the detector is
a high
impedance device and that any current that flows through it is
insignificant in comparison to Ix
(In fact, provided that the objective is to balance the bridge
rather than read the error voltage, such an assumption will never
cause any measurement errors because, at balance, the current
flowing through the detector goes to zero). We may then observe
that the two impedances Zx=Rx+jXx and Z0=R0+jX0
carry the same current, Ix,
and
that this establishes the phase relationship between V0, Vx, V0+Vx, and V1+V2. Also, we
may simplify the problem by choosing Ix
as the reference vector and setting its phase to be 0°,
allowing
it to be treated as a scalar Ix
= |Ix|.
Hence:
V0 = Ix Z0 = Ix (R0 + jX0 )
Vx = Ix Zx = Ix (Rx + jXx )
V0 + Vx = Ix [ R0 + Rx + j( X0 + Xx ) ] = V1 + V2
The only matter we have yet to establish is the relationship between V1 and V2, but to simplify the analysis, we will start by making the obvious choice of a voltage splitting network that produces V1 in phase with V2. Assuming that we also know the relative magnitudes of V1 and V2, we can then draw voltage phasor diagrams for the system, as below:
V0 = Ix Z0 = Ix (R0 + jX0 )
Vx = Ix Zx = Ix (Rx + jXx )
V0 + Vx = Ix [ R0 + Rx + j( X0 + Xx ) ] = V1 + V2
The only matter we have yet to establish is the relationship between V1 and V2, but to simplify the analysis, we will start by making the obvious choice of a voltage splitting network that produces V1 in phase with V2. Assuming that we also know the relative magnitudes of V1 and V2, we can then draw voltage phasor diagrams for the system, as below:

What is remarkable about the vector addition process that takes place, and that should be obvious by studying the phasor diagram, is that the bridge will not balance (i.e., Vdet will never reach zero) unless V0 and V1 (and also, by association, VX and V2) are equal in both phase and magnitude. This means that, despite the fact that there are two variable elements in the current-sampling arm of the bridge (R0 and X0), there is still only one way in which the bridge can be balanced once the relationship between V1 and V2 has been established. The balance condition for the bridge is:
| Zx = Z0 V2 / V1 |
Which is the same as for Christie's bridge, but with impedances substituted for the original resistances and all of the variables being converted into phasors. If V2 is in phase with V1, then the ratio V2/V1 is simply a real number |V2|/|V1| that scales Z0 to make it equal to Zx [AC Theory, 24.8]. If for some reason, we decide that V2 should not be in phase with V1, then we can analyse the chosen voltage splitting network to derive a complex-number expression for V2/V1, which can be substituted into the balance equation given above to maintain its validity.
What all of this means, of course, is that to balance the bridge, we must adjust R0 and X0 independently; and the series-equivalent impedance for Zx is given by:
| Zx = ( R0 + j X0 ) V2 / V1 |
If we arrange for V2 to be in phase with V1 then:
| Zx = ( R0 + j X0 ) |V2| / |V1| |
and if we arrange for V2 to be equal to V1 (in both magnitude and phase) then:
| Zx = ( R0 + j X0 ) |
This is obviously the basis for an Impedance Measuring Bridge. There are however, a few practical subtleties in the matter of designing impedance bridges; and before moving on to them, we will first discuss voltage-splitting networks, generators, and detectors.
5. Voltage Splitting Networks:
In the case of Christie's original bridge, the voltage-splitting network used (i.e., the pair of ratio arms) was simply a resistive potential-divider or a potentiometer. In the process of generalising the bridge to work with alternating voltages and currents, we simply replaced the unknown and the reference resistances with impedances. We now take this process to its logical conclusion by also replacing the voltage-splitter resistors with impedances. The relationship between the two voltages obtained may be deduced by constructing phasor diagrams according to the scheme outlined below, where the current I is the reference vector, and I=|I|:
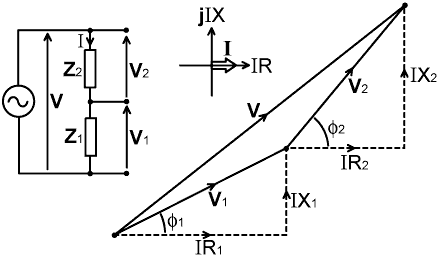
Fig. 5.1
|Z| = √(R²+X²);
and by Ohm's law, the magnitude of the voltage across an impedance is given by:
|V| = |I||Z| = I|Z|.
The relative magnitudes of V2 and V1 are therefore given by the expression:
|V2| / |V1| = |Z2| / |Z1|
The phase difference between V2 and V1 is simply φ2-φ1. where Tan(φ2)=X2/R2 and
Tan(φ1)=X1/R1.
The problem with this type of network is that reactance is frequency dependent, and so if we write down the general expression for φ2-φ1 we find that the phase difference between V2 and V1 will vary with frequency. This is acceptable if we are trying to design a bridge for operation on a single frequency, but such is usually not the case in the context of RF measurement. There is one important exception to this phase variability however, which occurs when we make φ2=φ1 with both impedances either capacitive or inductive (or purely resistive); i.e., we specify that the two voltages must be in phase at all frequencies, which means that the two impedances must follow the same frequency law. In this case, Tan(φ2)=Tan(φ1) and so:
| X2 / R2 = X1 / R1 |
In this expression, if we fill in the details of the reactances, i.e., X=2πfL if inductors are used, or X=-1/(2πfC) if capacitors are used, we find that the frequency dependent terms cancel, and that the relationship between V2 and V1 becomes frequency independent. This frequency independence will however only hold to the extent that the impedance versus frequency laws for the two impedances are identical, i.e., we are best off using near-ideal devices that can be modelled reasonably accurately as a pure resistance in series with a pure reactance. What the relationship says however, is not that the two impedances must be the same, but that the phase relationship will hold as long as the ratios X2/R2 and X1/R1 are the same. Thus we can, if we wish, make an unequal splitter that maintains the required voltage ratio over a wide range of frequencies. We might, for example, decide that we want V2 to be four times as large as V1, in which case we simply arrange things so that X2 = 4X1 and R2 = 4R1. Recall also that Qcomp = |X|/R, and so the phase relationship will hold over the range for which the Qs of the two arms of the voltage splitter remain the same.
Perhaps what is less obvious, but most useful of all, is that the phase and magnitude relationships still hold if the resistive components of the two impedances are allowed to become arbitrarily small. If we put R2 = 0 and R1 = 0 into the equation above, the result amounts to ∞ = ∞, which might appear problematic until we realise that if the relationship between V2 and V1 holds good as X2/R2 and X1/R1 become arbitrarily close to infinity, then it must hold good upon reaching infinity. Furthermore, as the resistance terms disappear, so does the requirement that the resistance must remain in strict proportion to the reactance. In other words, as the resistance terms disappear, V2 and V1 are forced more and more accurately into phase at all frequencies. This means, in principle at least, that we can construct potential divider networks using pairs of capacitors, or pairs of high Q inductors, which can do as good a job as a pair of resistors. There is one very good reason for wanting to do so; which is that reactive potential dividers do not consume any power, and so will not get hot if we are, for example, trying to divide or sample the voltage output of a large radio transmitter.
In view of the preceding argument, we can now specify three simple 'frequency-independent' voltage splitting networks that can produce two voltages in series, in phase, and in any ratio we may care to choose. We will now consider the practical merits of these three networks in turn:
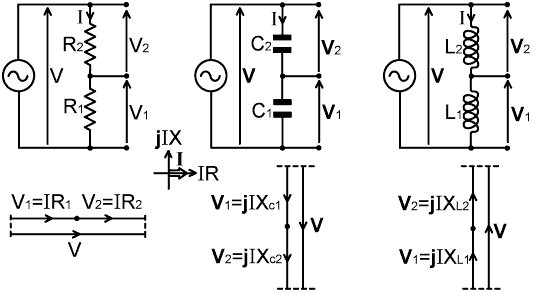
Fig. 5.2. Basic voltage-divider networks.
Capacitors are inherently high-Q devices when correctly chosen for the job in hand, and so capacitive potential dividers are capable of good phase accuracy. Component tolerances are generally broader than for resistors however, and any stray capacitances will be absorbed into the network. Consequently it may be necessary to place a trimmer capacitor across one of the capacitors so that the voltage ratio can be adjusted to the required value. Capacitors consume no power (neglecting losses) but the reactance of the network varies with frequency. At very low frequencies, the reactance becomes extremely high, leading to low output current capability (from the junction between the two capacitors) and consequent insensitivity of the bridge. As the frequency is increased, the reactance falls, and a point will be reached when the network presents an unacceptably reactive load across the generator. Care must therefore be taken in the choice of capacitor values, but a working range of 4 octaves or more is possible in RF applications. We may also, of course, place resistors in series with the capacitors (in appropriate proportion to the reactance, as mentioned previously) in order to limit the minimum impedance presented to the generator at high frequencies; or we may place suitably proportioned resistors in parallel with the capacitors in order to assist the output at lower frequencies. In the latter case, the network can be designed using the simple observation that if a reactive network designed to give a particular voltage output is placed in parallel with a resistive network designed to give the same output voltage; then the off-load voltage will be unchanged, but the output impedance will be lower (i.e., the network will be less susceptible to loading effects). If resistors are added to the network, of course, their parasitic reactances must be taken into account. The capacitors also must either have very small or proportionate parasitic inductances. A small compensating inductance is sometimes placed in series with one of the capacitors if the arms of the voltage divider are not physically identical.
The use of capacitive ratio arms in RF impedance monitoring applications was adopted by the Collins Radio Company in the 1950s, and the resulting configuration is referred to in the manuals of that period as a "modified Schering bridge". The original Schering bridge that gave rise to the idea is a high-voltage test-set for measuring the the dielectric losses of capacitors [4]. Other authors [5], [6], refer to the capacitive ratio-arm bridge as the "Micromatch", and the "De Sauty - Wein" Bridge. In fact, the configuration resembles the De Sauty bridge, but to name it so in this context would be to miss the point; which is that the need to replace the arms of Christie's bridge with impedances is obvious within a particular field of application, and just about every possible bridge configuration that can be obtained by so doing is named after someone [4], [7]. The author's preference is to refer to the device generically as a "CRAB" (capacitor ratio-arm bridge).
"Modified Schering bridge" (capacitor ratio-arm bridge) used as a mismatch indicator in the 1950s vintage Collins 180L-2 and 3 automatic antenna tuners.
Refs:
[4] Electrical Measurements and Measuring Instruments, E. W. Golding. 3rd edition, Pitman, London, 1949.
Schering bridge, p154-158. De Sauty bridge, p214-216.
[5] "Measuring RF Power", Joe Carr [K4IPV], Electronics World, Nov. 1999 p942-948. Dec 1999 p1000-1005.
Part 1: Definitions and dB notation, thermistors, bolometers, thermocouples, diode detectors. In-line bridges: Micromatch [Christie with capacitive ratio arms], Monomatch (sic) [two types: Coupled transmission lines. Current transformer with capacitive voltage sampling, current summing configuration]. Part 2: Bird 'Thruline' wattmeter. Calorimeters. Micropower measurement techniques. Mismatch loss and mismatch uncertainty.
[6] The ARRL Antenna Book, 19th edition, ARRL publ, 2000. ISBN: 0-87259-804-7.
Bridge types, p27.4.
[7] Modern Impedance Measurement Techniques, Alan Bate, Electronics World, Dec. 2002, p12-18. Jan 2003, p18-25. Feb 2003, p49-56. Mar 2003, p52-59.
Review of professional impedance measurement techniques: Basic bridges. Three-terminal measurements. Bulk metal film reference resistors. Guard amplifiers. Phase sensitive detectors.
[xx] Radio Engineers Handbookk, F E Terman, 1943, sect. 13, p902 - 911: Common bridge types.
5a. Inductive voltage splitters:
Although the capacitor ratio-arm bridge is attractive for monitoring the output of radio transmitters, progress in the design of bridges for accurate impedance measurement depended on a move away from the idea of discrete or non-interacting arms. The first step in this direction is to consider what happens when the ratio arms are replaced by inductors.
Of the basic passive electronic components, inductors are the least well-behaved. They have substantial RF resistance, which varies with frequency, and they have substantial self-capacitance, which may easily give rise to self-resonance in the frequency-range of interest. Air-cored inductors are also sensitive to environmental factors, they are difficult to make accurately, and the introduction of adjustable magnetic cores (slugs) may give rise to further frequency dependent variations of reactance and resistance. Inductors might therefore seem to be the least prepossessing of candidates for construction of voltage dividers; that is, until we allow mutual inductance between the two coils and turn the assembly into an auto-transformer.
If the sense of the windings of the two coils is the same, mutual inductance increases the inductance of the series combination and initiates transformer action. This allows us (in principle) to have the best of both worlds: a large inductance across the generator to minimise standing current, and a low impedance output from the tapping point to maximise detector sensitivity. If the magnetic coupling between the windings is tight moreover, then the output voltage ratio is precisely defined by the turns ratio, i.e., (referring to the left-most diagram below): |V2|/|V1|=N2/N1, and the two voltages are in phase. This configuration was invented in 1926 by Alan Blumlein, the coupling being achieved by means of twisted-bifilar winding. Blumlein, having a knack for catchy titles, called his invention "the closely-coupled inductor ratio-arm bridge" [8]. Further improvement in the coupling is nowadays achieved by using a closed magnetic path between the coils, e.g., by winding them (bifilar) on a high-permeability ferrite toroid. Extremely wide bandwidths are possible, the lower frequency limit being dictated by insufficient inductive reactance and consequently excessive standing current, and the upper frequency limit being dictated by self-capacitance effects and core losses. Design data for ferrite-cored toroidal coils is given in Section 6.2-12.
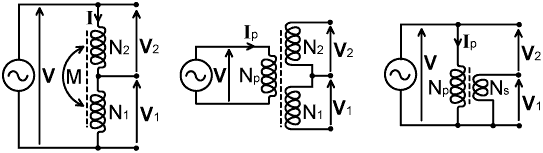
In the central diagram above, we take the inductive splitter idea to its logical conclusion by using a true transformer. A bridge based on such an arrangement is known as a 'transformer ratio-arm bridge' (TRAB), and this approach was developed in the 1940s by Gilbert Mayo of the BBC Research Department [50], [LE300/A handbook]. A true transformer gives the additional benefit of DC isolation from the generator, and permits optimisation of the loading relationship between the generator and bridge network.
The auto transformer and the tapped isolation transformer have the advantage that any imperfections in behaviour manifest themselves in both outputs, and so tend to cancel. The third option (above right) therefore appears to be less promising, because any phase or magnitude errors in the transformer output V1 will be transferred into the relationship between V2 and V1. Such errors can be taken into account however, provided that the transformer is operating within a defined pass-band; and compensation for residual errors is possible. Later on moreover, we will return to the point that the purpose of the voltage splitter is not to provide a power supply, but to establish the ratio between a voltage sample and a current sample. If the ratio can be established in some other way (which it can) then only one voltage sample is required.
The resistive, capacitive, and transformer voltage splitting networks introduced above should be regarded as the basic building blocks for the ratio arms of Wheatstone-Christie or Blumlein bridges. Later on however, when we start to deviate from the Wheatstone topology, we will return to the idea of using voltage sampling networks that have frequency dependent outputs; not so that we can make bridges that are unnecessarily complicated and difficult to understand, but so that we can tailor the frequency response of the voltage sampling network in order to compensate for the amplitude and phase errors in the output of the current sampling network.
Refs:
[8] The Inventor of Stereo: The Life and Works of Alan Dower Blumlein, Robert Charles Alexander, Focal Press 1999. ISBN 0 240 51577 3.
See also: British pat. no. 323037.
[50] Mayo
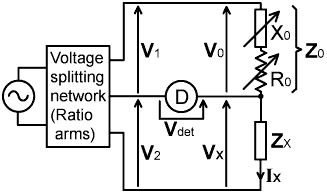
Generators and Detectors:
The determination of the resistive and reactive components of an impedance requires that a measurement should be made at a single frequency. This can be accomplished in the obvious way, by using a narrow-bandwidth (i.e., sine-wave) generator and a broadband detector; but it can also be done the other way around, i.e., by using a wide-band generator and a narrow-bandwidth detector. In the latter case, the generator can be either a noise source, or a comb-spectrum source (i.e., a low-frequency signal rich in RF harmonics), and the detector a radio receiver. When using a broadband source, it does not matter that the bridge will only balance at one of the frequencies contained in the generator output, because the bridge is a linear network, no mixing occurs, and the detector will only indicate the bridge condition at the frequency to which it is tuned. In general however, sine-wave generators of reasonably high output are easiest to use.
The most obvious source to use in conjunction with a wideband detector is an RF signal generator, which should have a low level of harmonics in its output. Before making an expensive purchase however, or embarking on a time-consuming construction project, it should be noted that basic bridge measurements do not require an accurate knowledge of the generator output level. Only the frequency needs to be known accurately, and an ordinary radio transceiver is a perfectly capable signal generator in this respect. The principal drawbacks in using a radio transmitter as a signal generator are that the output may be rather large, and fussy with regard to load impedance, and the frequency coverage of transceivers intended for amateur use is not usually continuous. Such problems are generally surmountable however, as we shall now discuss.
The vast majority of modern commercial all-band HF amateur-radio transceivers use power amplifiers based on circuits originally developed by Helge Granberg (K7ES, OH2ZE) of Motorola inc. [9]. These are broadband push-pull transformer-coupled amplifiers that operate from 1.6 to 35MHz or more, but give relatively high levels of odd-order (3rd, 5th, 7th, etc.) harmonics. The amplifier output must therefore be routed through a low-pass filter selected to give appropriate harmonic suppression for the frequency of operation. Complete HF coverage requires seven or eight low-pass filters, switched by means of relays operated by the system microcontroller, and the amateur frequency allocations are such that complete amateur coverage requires a full HF set of filters. Obtaining general transmitter coverage is therefore often a matter of removing restrictions rather than adding functionality; the restrictions being applied by means of one or more 'transmit-inhibit' signals from the microcontroller, which usually disable a driver amplifier. Modifications, firmware updates, or special keypad sequences that disable the legal-restriction signals are usually known to the manufacturer's service agents, and might be released to those who have legitimate reasons for requiring general transmitter coverage. Alternatively, for those with sufficient knowledge of radio circuitry, it is possible to devise appropriate modifications by studying service manuals; and documents describing modifications can often be found via the Internet. Caution is advised with regard to information obtained from the Internet however, and the actual effect of any proposed modification should be assessed carefully by studying the transceiver circuit diagram. Transceivers that have a transverter socket can almost certainly be modified, because the transverter output usually is a general-coverage signal, and the point at which the transmit-inhibit signals are applied must be in a part of the signal-chain that lies after the transverter take-off point. The low-level transverter output (a few hundred millivolts RMS) will also be sufficient on its own if an additional radio receiver is used as the detector.
One advantage of using a radio receiver as the detector is that it will have an approximately logarithmic input response, due to the action of tha AGC system. When making impedance measurements, a logarithmic detector response facilitates the location of the null because the level indicator is never off-scale [See Hatfield LE300A Manual]. It is necessary to use a 'fast' AGC setting incidentally.
When testing transmission bridges, the author uses an old Kenwood TS430S 100W HF transceiver as a high-power signal generator. This unit can be tuned while transmitting, and can be converted to give continuous transmitter coverage from 1.6 to 30MHz by the simple expedient of unplugging connector 10 on the RF circuit-board.
For a measuring bridge with a simple passive diode detector, an appropriate supply voltage is usually in the order of 5 to 20 V RMS. This, as we shall see, is sufficient to ensure acceptable detector linearity, and is low enough not to exceed the reverse-voltage rating of the ubiquitous 1N5711 Schottky diode (Vr m=70 V). A 100 W transmitter designed for a 50 Ω load, on the other hand, produces a nominal maximum output voltage of 70.7 V RMS ( V = √(PR) = √(100×50) ) and may not give full output or proper harmonic attenuation unless its load impedance is in a range that corresponds to an SWR of better than 1.4:1. This means that the transmitter prefers a load resistance of between 36 and 70 Ω (i.e., 50/1.4 and 50×1.4 Ω); and since the output impedance of a transistor transmitter is usually lower than the design load resistance, coolest running will be obtained if the load resistance cannot drop greatly below 50 Ω. When using a transmitter to power a bridge therefore, an intervening network is required in order to reduce the maximum available voltage and swamp any reactive impedance that the bridge may present. Such a network might take the form of a resistive potential divider, of total resistance not exceeding 70 Ω, rated to handle the full transmitter output, and designed to give 10 V RMS with the transmitter operating at about half-power.
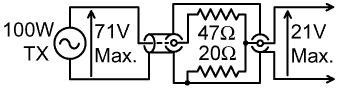
>A suitable potential divider network is shown above. This can be built using bulk-metal-foil (Vishay) or other non-inductive resistors, the appropriate power ratings being ≥70 W for the 47 Ω resistor, and ≥30 W for the 20 Ω resistor. A suitable 47 Ω resistor is the Meggitt BDS100-47R (RS Stock No. 225-1193), and a suitable 20 Ω resistor is the Vishay MP930-20R (RS stock No. 320-4980). Both resistors must be mounted on a large heatsink. When using a potential divider of this type incidentally, take care not to exceed the transmitter's continuous output rating for more than a few seconds (usually about 50 W, consult the manual), and keep the potential divider away from anything that might be affected or damaged by heat. Also note that if the impedance to be measured is an antenna, a small signal will be radiated, and it might be more appropriate to use a low-level generator and a radio receiver for measurements.
References:
[9] Radio Frequency Transistors, Norm Dye and Helge Granberg. Motorola inc. / Butterworth Heinemann, Newton MA. 1993. ISBN 0-7506-9059-3.
See also: Diode detectors for RF measurement. DWK
© D W Knight 2007.
David Knight asserts the right to be recognised as the author of this work.
