Optical magnification

Optical Magnification

By David Knight

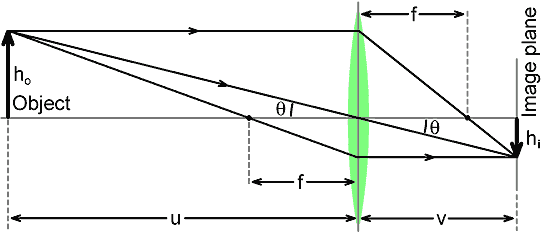
Thin lens formulae
For those who use cameras and lenses (as apposed to those who design them), most calculations relating to field-of-view (FOV) and magnification can be performed by using the concept of the idealised equivalent symmetric thin lens. A converging (bi-convex) lens of this type is depicted below, with its attendant ray diagram. Note that, since the lens is symmetric, it works the same regardless of which way the light is travelling. Thus it has two focal points, one on each side, both at distance f (the focal length) from the plane of the lens. The focal point is defined as the point at which an ideal lens brings light from infinity to a focus.

The idealised converging lens has the following properties:

1) Light rays travelling parallel to the axis are deflected in such a way as to make them pass through a focal point (and light rays passing through a focal point are deflected to run parallel to the axis)

2) Light rays passing through the centre of the lens are undeflected.

The first condition follows from the definition of the focal point. The second condition arises because the front and back surfaces at the centre of the lens are parallel, so that the deflection of the ray as it enters the glass is reversed as it leaves the glass. Since the lens is thin (and especially if the ray is nearly perpendicular to the surface, the lateral displacement on passing through the glass is negligible. Taken together, the two conditions give rise to the thin lens formula:

. . . . . . . .

(1)

where u (the 'object distance') is the distance from the object to the lens plane, and v (the 'image distance') is the distance from the image to the lens plane. 'Proof' of this relationship is given by the boundary conditions (i.e., by what happens at the extremes of the possible values of u and v). Thus when u→∞, 1/u→0 and v=f. Similarly, when v→∞, 1/v→0 and u=f. In other words, the formula arises because the lens brings light from infinity to a point.
The magnification due to the lens is defined as the height of the image divided by the height of the object:

m = h_i / h_o

but, looking at the diagram we can see that:

Tanθ = h_o / u = h_i / v

which tells us that

h_i / h_o = v / u

i.e.;

m = v / u

(2)

We can also obtain more formulae for the magnification as follows:
Firstly, multiply equation (1) throughout by v. This gives:

(v/u) + (v/v) = v/f

i.e., substituting for v/u using (2):

m + 1 = v/f

hence:

m = ( v / f ) - 1 = (v - f) / f

(3)

also, we can multiply equation (1) throughout by u, which gives:

1 + 1/m = u/f

i.e.,

m = 1 / [ (u/f) -1 ]

which, upon multiplying top and bottom of the right hand side by f gives:

m = f / (u - f)

(4)

Unit magnification
From equation (2) we can see that unit magnification (m=1), also known as the 1:1 macro condition, occurs when v = u. If we put this into equation (1) we get:

2 / u = 1/f

i.e.:

u = v = 2f

Unit magnification occurs when the lens is placed at a distance of twice the focal length from the image plane (note however, that this rule only applies to symmetric lenses).

Practical camera lenses
Unfortunately, simple thin lenses do not bring light rays from a point on the object to a perfect point in the image. There are numerous optical defects, such as spherical aberration and chromatic aberration, and these place a limit on the sharpness of the resulting image. Hence lens designers add extra elements (i.e., extra simple lenses), with a view to cancelling the various aberrations to some acceptable degree. These attentions bring the system closer to the ideal in terms of ray convergence, but the resulting compound lens is no longer thin.
The camera lens designer must also work to the specification of the lens mount, which means that some lenses, particularly wide-angle types, cannot be made symmetric when the distance from the exit aperture to the image plane is greater than the required focal length (the lens must be able to focus at ∞). A further consideration is that digital camera sensors suffer from sensitivity fall-off for light rays arriving at angles far from the perpendicular, and the solution to this problem is to design the lens so that emerging rays appear to come from a point a long way from the sensor (often well in front of the camera).
The aperture towards which light rays from outside the camera must be directed in order to form an image is called the 'entrance pupil'. The aperture from which light rays appear to emerge is called the 'exit pupil'. The pupils usually correspond to the apparent position of the iris when looking into the respective side of the lens (but not necessarily to the physical position of the iris). The practicalities of camera lens design, as well as often demanding that the front and back focal lengths are different, almost invariably demand that the entrance and exit pupils do not lie in the same plane. The result is that the object-side (front) and the image-side (back) optical systems become physically disconnected, as shown in the diagram below.

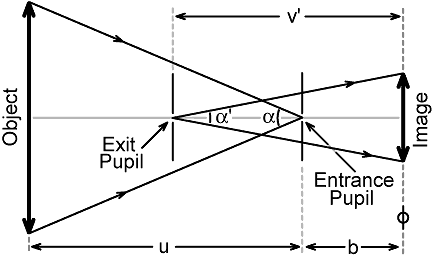
Note that, in general, the object side field-of-view (α) does not have to be the same as the image side FOV (α'). In particular, in the case of a wide-angle lens, it is usually important that α' << α (to avoid sensor fall-off, to allow room for an SLR mirror, etc.). The designer nevertheless can calculate the angle α that corresponds to the image just filling the diagonal of the format, and this can be converted to an equivalent symmetric-lens focal length using a formula given in the angle of coverage article, i.e.:

f = d / [ 2 Tan(α/2) ]

where d is the format diagonal. Note that f is a true focal length in the sense that a light ray passing through the front focal point (on the object side) will emerge parallel to the axis on the image side. The lens however, will not necessarily focus light from infinity (on the object side) to a point at a distance f (on the image side) from either the entrance or exit pupil.
The consequence of the spatial disconnection between the front and back optical systems is, from the camera user's point of view, surprisingly minimal. We can remain blissfully unaware of what goes on inside the camera and perform calculations relating to external optical systems (lens ports, supplementary lenses, etc.) on the basis that there is a symmetric thin lens of focal length f located at the entrance pupil. The only caveat is that it is no longer possible to determine the position of the image plane from the object distance and the front focal length f. We do need to know where the image plane is however, because it dictates where the entrance pupil will end up when we mount the camera (e.g., on its tray inside an underwater housing), and because the distance markings on the lens (and the minimum focusing distance) are specified relative to the image plane. For that reason we need to determine an additional parameter b (the back focal distance), which can sometimes be obtained from the lens literature, but must otherwise be estimated.
On cameras with interchangeable lenses, the image plane (also called the 'focal plane') is often marked with the symbol fp_mark

. The reason why optical measurements are given relative to the image plane is that it is a fixed reference relative to the lens mount, whereas the entrance pupil moves as the lens is focused or zoomed.
A final point, of which most photographers will already be aware, is that since we don't need to know the details of the back optical system, we are at liberty to use any value of format diagonal we care to choose in order to obtain the focal length equivalent to the FOV. A common choice is to use the diagonal of the 35 mm stills format (43.267 mm), so that our equivalent focal lengths correspond to familiar properties (<28 mm is wide, ca. 50 mm is normal perspective, 80 mm is portrait and ≥135 mm is telephoto). We can also, for every format, work out a 'crop factor', which is a number by which the actual focal length of a lens must be multiplied in order to obtain the 35 mm equivalent focal length. The crop-factor for the Four-Thirds format, for example, is 2; which means that (say), a 50 mm lens acquires a 35 mm equivalent focal length of 100 mm.

DWK

Photography & Optics