|
|
|
 |
 |
5. Impedance Matching. Part 1.
By David Knight G3YNH and Nigel Williams G3GFC
Contents:
|
5-0. Introduction. 5-1. Z-plane operations. 5-2. Series reactance and resistance. 5-3. Parallel impedance. 5-4. Admittance, conductance, susceptance. 5-5. Equation of a circle. |
5-6. Parallel resistance (constant B). 5-7. Parallel reactance (constant G). 5-8. Transformers (constant f) 5-9. Impedance matching strategies. 5-10. Z-plane domains. 5-11. The Match Meter. |
|
Introduction: Having shown in previous chapters how an antenna system can be reduced to a two-terminal network and considered simply as an impedance; we now look at the impedance matching process. In previous chapters it was shown how an impedance can be brought to resonance by means of a conjugate series reactance, and thereby converted into a pure resistance. The full impedance matching process however, is a two-step operation, which involves both reactance cancellation and resistance transformation; the object of the exercise being to convert an arbitrary impedance to a specific desired value of resistance. The usual target resistance value is 50W, which is the preferred load resistance for modern transistor power amplifiers and also an entirely suitable load resistance for most valve (tube) amplifiers. The information which follows however, is readily adaptable to target resistances other than 50W. Impedance matching is, of course, carried out by means of an antenna tuner or 'ATU'. It must be stressed however, that the type of antenna tuner under discussion is not the type which is often built-in to a transceiver. A typical 'built-in' ATU in a modern transistor transceiver might have a matching range of about 17 to 150W resistive, and about ±300W reactive. This is sufficient to make a coax-fed resonant antenna usable over a whole amateur band, and is also useful for matching the input impedance of a valve (tube) linear amplifier (which is unlikely to be exactly 50W), but is entirely inadequate for matching the vast range of input impedances which can be presented by a general coverage antenna system. Likewise, the output p-coupler of a valve amplifier is likely to have a restricted matching range, and may not give adequate harmonic attenuation when used to match loads vastly different from 50+j0 W. The antenna tuners of interest here therefore are what might be called 'full-range' matching networks, i.e., tuners with a range of about 3 to 3000W resistive and ±2500W reactive. The adjustment procedures for common antenna tuners will be discussed later in this chapter; but first we will lay the basis for an understanding of such procedures by examining the effects of the electrical components involved. Antenna tuner adjustment is usually carried out with the aid of an SWR meter; but as we shall see, SWR is not the best quantity to monitor during the adjustment phase, and an alternative measuring bridge, not much more complicated than an SWR bridge, can lead the operator directly to the most efficient matching solution for a given type of matching network. |
|
5-1. Z-Plane Operations: The impedance matching process is best considered as a set of operations in the impedance plane, or Z-plane. The Z-plane is simply a graph of R against jX on which a given impedance can be plotted as a point. The Z-plane therefore corresponds to a mathematical space; impedance space, in which all impedances can be considered to lie. A matching network can be regarded as a toolkit of components which can be combined with an impedance in some fashion in order to move the resultant impedance to a new position in the Z-plane.To represent this process, we will use the notation: Z ® Z' which is pronounced: "Z goes to Z prime", or "Z becomes Z prime". The prime symbol is generally used to indicate modification, i.e., Z' is different from Z but is related to it because it results from an operation performed on Z. In general, impedance matching is a matter of manipulating the point Z by the addition of some combination of transformers and series and parallel impedances. In practice, for reasons of efficiency, and especially in the case where the impedance to be matched is an antenna system; the manipulation is performed using only high Q coils and capacitors, and any transformers used should preferably be transmission-line transformers. |
|
5-2. Series Reactance and Resistance: The simplest operation which can be carried out on an impedance is to place a resistance or reactance in series with it. As was discussed in chapter 1; if a pure resistance is placed in series with an impedance Z, it simply adds to the R-part of Z without affecting the X-part. If a pure reactance is placed in series with Z it adds to the X-part without affecting the R-part. Thus if an impedance Z=R+jX has a reactance XS placed in series with it, the new impedance is Z'=R+j(X+XS). If Z has a resistance RS placed in series with it, then Z'=(R+RS) +jX. The effect of these operations in impedance space is shown below: |
|
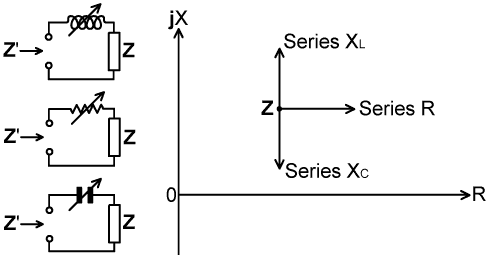
Note that while we can only add resistance (so moving
Z to the right), we can add or subtract reactance, because
inductors and capacitors have opposite effects, and so move freely
up or down in the vertical direction. Vertical lines in the Z-plane
(i.e., parallel to the jX axis) are known as lines
of constant resistance. Horizontal lines (parallel to
the R axis) are known as lines of constant reactance. Note that if an inductor is used, increasing L (and hence XL) moves Z' upwards. If a capacitor is used however, reducing C (increasing the magnitude of Xc) moves the Z' downwards, i.e., a series capacitor must be initially large to have no effect, and its effect increases as its capacitance is reduced. Resistance, of course, is not normally used for antenna matching purposes; but in situations where a moderate loss of power is acceptable or desirable, such as in matching the input impedance of a linear amplifier, there may be reason to include it in the matching network. Understanding the effect of resistance is also important for an understanding of the effect of real components, particularly inductors, which often have substantial loss resistance at radio frequencies. |
|
5-3. Parallel Impedance: In section 1.11, in setting out the basics of AC electrical theory, we derived what might be called a 'brute-force' solution to the problem of finding out what happens when impedances are connected in parallel. The resulting expression is shown below for an impedance Zp=Rp+jXp placed in parallel with an initial impedance Z=R+jX, i.e., it is the expansion of the parallel impedance formula Z'=ZZp/(Z+Zp).
This equation, while possesing a certain symmetry, offers a version of what is happening which is extremely difficult to visualise; and even hardened mathematicians like to think in pictures. There is a better way of looking at the problem however, which involves re-defining it in terms of the reciprocal of impedance, i.e., 1/Z, this quantity being known as admittance. This alernative approach (which is the basis of the Smith chart) does not particularly simplify the expressions we need to use when writing computer programs or performing spreadsheet analyses, but it scores on two major points: it allows us to view the parallel impedance problem as a simple matter of addition, and it allows a straightforward graphical way of visualising the effect of placing a resistance or a reactance in parallel with an impedance. |
|
5-4. Admittance, Conductance, and Susceptance. The subject of admittance was introduced in section 1-36. There we defined admittance as Y=1/Z, where, as usual, Z=R+jX. From this we obtained the relationship: Y = (R - jX) / (R² + X²) which can be written Y = G + jB where the real part of the admittance, G, is called the conductance, and the imaginary part of the admittance, B, is called the susceptance (of the network under consideration). Hence the definitions for conductance and susceptance are: G = R / (R² + X² ) B = -X / (R² + X² ) Now observe that if a network is purely resistive, it has no susceptance, i.e., Y=G+j0. Consequently, if we place a pure resistance Rp (with Gp=1/Rp) in parallel with an impedance Z (with Y=1/Z) the resultant admittance is given by: Y' = ( G + Gp ) + jB. This means that, no matter what value the parallel resistor takes, it cannot alter the original value of susceptance. The resultant impedance is therefore constrained to follow a path of constant susceptance as the parallel resistance is varied. Similarly, if a network is purely reactive, it has no conductance, i.e., Y=0+jB. Consequently, if we place a pure reactance Xp (with Bp=-1/Xp) in parallel with an impedance, the modified admittance is: Y' = G + j( B + Bp ) Which indicates that the parallel reactance cannot alter the original value of conductance, and the resultant impedance must therefore be constrained to lie on a path of constant conductance. It transpires that when susceptance or conductance is held constant, the path on which an impedance is constrained to lie takes on a very simple form. The curve in question was no doubt discovered (many years ago) by someone who plotted a graph of it the hard way (using the parallel impedance equation) and became suspicious of the shape. Here we will pre-empt the discovery, by exploring the properties of the simplest object which can be drawn using a pair of compasses. |
| 5-5. The Equation of a Circle. |
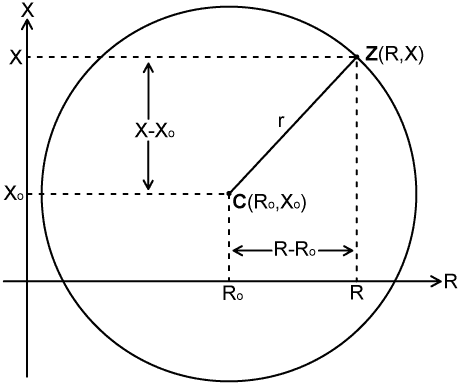
The diagram above shows a circle of radius r, with its centre
C placed arbitrarily at a point (Ro,
Xo). In order to produce an equation for
this circle (an hence any circle), all we have to do is write
an expression for the radius which is true regardless of how
we measure it; i.e., regardless of where we put the point Z
from which the distance from C to Z (the radius)
is measured. Since r is the hypotenuse of a triangle with sides
X-Xo and R-Ro,
the equation is given by Pythagoras' theorem, i.e.:
|
|
5-6. Parallel Resistance: Earlier in this chapter (from a derivation given in section 1-11), a general expression was given for the impedance which results when two impedances are placed in parallel. If one of the impedances is purely resistive, the expression reduces to:
The effect of a resistance Rp in parallel with an impedance Z=R+jX can also be considered as the effect of a conductance Gp=1/Rp in paralell with an admittance Y=G+jB, in which case: Y' = G + Gp +jB. Since the susceptance B=-X/(R²+X²) is completely defined by the original impedance, it remains constant regardless of the value of Rp. Therefore we may also write: B = B' = -X' /( R'² + X'² ) i.e., the new susceptance is the same as the old susceptance. This equation may be rewritten:
Compare this with the general equation of a circleof radius r with its centre at Ro,Xo (with the variables changed to X' and R' to suit the current problem): R'² + X'² -2R'Ro -2X'Xo + Ro² + Xo² - r² = 0 Note that in expression (5-6.2) there is no term equivalent to -2R'Ro, and so Ro must be zero; which means that the centre of the circle lies on the X axis. This reduces the circle equation to: R'² + X'² -2X'Xo + Xo² - r² = 0 There are no terms equivalent to Xo²-r², therefore Xo²=r², therefore Xo=±r. The circle just grazes the point R=0, X=0. Finally, we may equate -2X'Xo=X'/B, i.e., Xo=-1/(2B). Therefore the centre of the circle lies at Ro=0, Xo=±1/(2B) (there being two alternatives depending on the sign of X in the original impedance), and the radius is 1/(2B). The conclusion is that when a resistance Rp is placed in parallel with an impedance Z=R+jX, the resultant impedance Z' moves on a circle, which has its centre at 0-j/(2B), and a radius of 1/(2B), where B=-X/(R²+X²). Z' is constrained to lie between the original impedance R+jX and 0+j0, and since R is always positive, the curve is only part of a circle (an arc) and so is called an arc of constant susceptance. |
|
|
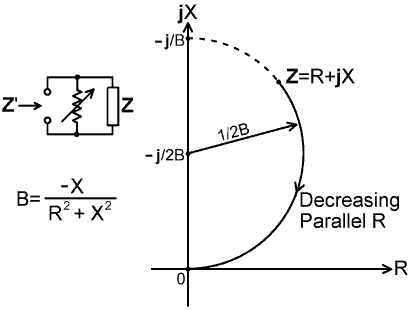
In the diagram above, the curve is shown for positive X (and
hence negative B). If X is negative, the curve has the same shape
but is reflected about the R axis. Note that if X is greater
than R, reducing the parallel resistance can actually cause the
resistive component of the resultant impedance (R') to increase
to a maximum of |1/(2B)| when X'=±j/(2B). The effect
of Rp however, is always to reduce the
load phase angle, i.e., it has the effect of swamping the reactance,
but it can never bring the phase angle to zero except at 0+j0. To give an idea of the rate at which Z changes as the parallel resistance is reduced, the table on the right shows computed values of R' and X' for various values of parallel resistance, Rp, connected across an initial impedance of 100+j100 W. Equation (5-6.1) was used for the calculation. Notice, in this instance, that the parallel resistance has little effect on the resistive component of the resultant impedance, R', provided that it is about 10 or more times greater than the initial resistive component R. In general, when the initial reactance X is large in comparison to R, parallel resistance has a stronger effect on X' than it does on R', but this is no longer true when X is small. |
|
|
Thus we conclude that the effect of adding reactance in parallel
with an impedance is to move the point Z' around a circular
path. The circle so described has its centre on the R axis at [1/(2G)]+j0, just touches the origin of the graph (0+j0), and is known as a circle of constant conductance. |
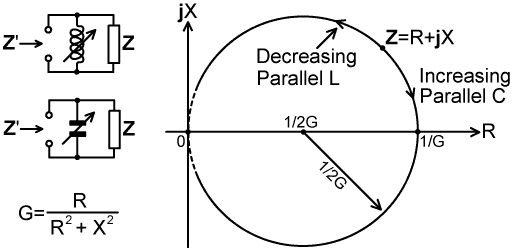
| The direction of rotation in the Z-plane is clockwise when a capacitor is connected across Z and anticlockwise when an inductor is connected across Z. The effect of a parallel reactance is least when the reactance is at its highest value, and increases at the reactance is reduced. Consequently, if a variable capacitor is used, increasing its capacitance (reducing Xc) moves the resultant Z in a clockwise direction; and if a variable inductor is used, reducing its inductance (reducing XL) moves the point Z in an anticlockwise direction. Note that the point 0+j0 is only approached if the parallel capacitance becomes infinite (Xc®0), or the parallel inductance goes to zero (XL®0), both situations corresponding to an effective short-circuit. |
| 5-8. Transformers: |
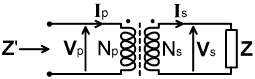
| In section 1-33, we showed that the effect of a tightly coupled conventional transformer, to a good first approximation at least, is to carry out an impedance transformation according to the square of the turns ratio. |
 |
|
Z' = ( Np / Ns
)² Z Thus a transformer scales the load impedance by a factor (Np/Ns)², where Np is the number of turns in the primary winding, and Ns is the number of turns in the secondary winding. This operation moves the resultant impedance Z' along a line starting at 0+j0 and passing through the original impedance Z. The transformer modifies the magnitude of the impedance but leaves the phase angle f unchanged, thus the resultant impedance is constrained to lie on a line of constant phase. |
|
This type of transformation can be achieved using both conventional
and transmission-line transformers; but transmission-line transformers
are to be preferred on the grounds of efficiency, bandwidth,
and freedom from core-saturation effects. Any transformer included
in a matching unit will also normally carry out a balanced to
unbalanced load transformation if required, i.e., the transformer
is also the balun. Dr Jerry Sevick, W2FMI (see references [1] - [8]) has described highly efficient wideband toroidal cored baluns and ununs, with impedance ratios of 1:1, 4:1, 9:1 and 16:1 (i.e., turns ratios of 1:1, 2:1, 3:1 and 4:1), and slightly less efficient intermediate ratios. When feeding a dipole antenna, a 1:1 balun is normally used, but other ratios can be convenient for shifting awkward impedances into different parts of the Z-plane. |
|
5-9. Impedance Matching Strategies: From the above, it can be deduced that the process of matching an impedance to (say) 50W, without introducing unnecessary losses, is a matter of manipulating the transmitter (generator) load Z' on to the point 50+j0 by moving it along lines of constant resistance and around circles of constant conductance. A switchable transformer gives the added possibility of moving Z' along a line of constant phase. All of the possible operations not involving resistance are summarised in the diagram below: |
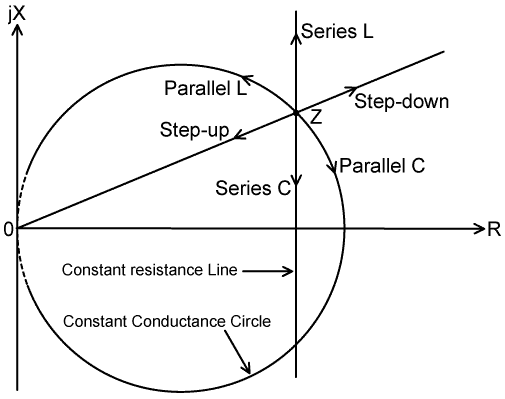
| Thus we are free to move anywhere in the Z-plane, but constrained in terms of the paths that can be taken. In order to work-out which operations should be used, we will consider the problem backwards by observing the attributes of the target impedance, i.e., 50+j0 W: |
|
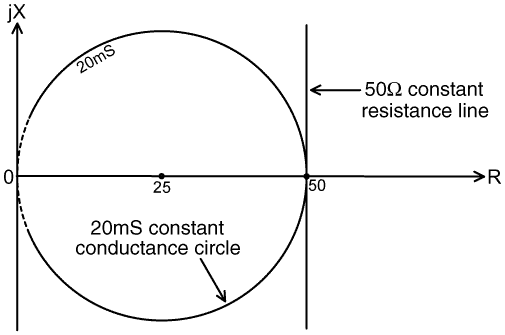
The first point to note is that the target impedance, 50+j0
W, lies on the 50W
constant resistance line. An initial impedance Z which
does not lie on this line can always be brought on to it by moving
it around a circle of constant conductance, i.e., by placing
a reactance in parallel with it. An intermediate impedance which
lies on this line can always be brought to 50+j0 by placing
a reactance in series with it. Therefore impedance matching can
always (in principle) be carried out in a two-step operation. The constant conductance circle on which 50+j0 W lies is known as the 20mS constant conductance circle (i.e., 20 milli-Siemens or 1/50 Siemens). Its radius 1/2G=25W, and its centre lies at the point 25+j0 W. It crosses the resistance axis at 0 and at 1/G=50W. If an initial impedance has a resistive component of less than 50W, it can always be manipulated onto the 20mS constant conductance circle by placing a reactance in series with it. An intermediate impedance which lies on the 20mS circle can then always be brought to 50+j0 by placing a reactance in parallel with it. |
|
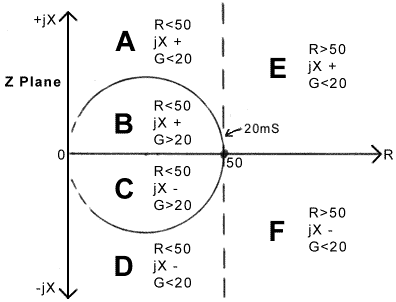
5-10. Z-Plane Domains: The diagram below shows six regions of the Z-plane, identified according to their relationship to the target impedance 50+j0. It also shows some of the matching networks which give the shortest possible route to Z=50+j0. The encircled numbers indicate the operations which must be performed, the order in which to perform them, and their effects. It is assumed that parallel reactances are initially set to their highest possible values (effective open circuit), and series reactances are initially set to their lowest possible values (effective short circuit). |
|
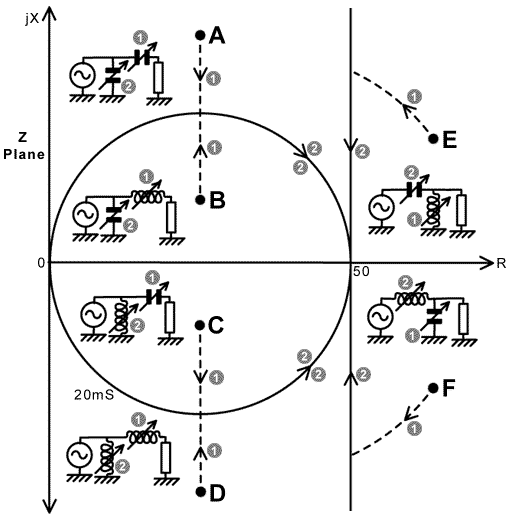
The diagram immediately shows why controversies exist over the
choice of best general purpose matching network. The reason is
that there isn't one. All of the popular matching networks will
do the job however, provided that there is sufficient adjustment
to force the initial impedance into a different region. For example,
region E might be a job for a T-match tuner with the antenna-side
capacitor set to maximum. If we must use a p-match
however, we can use the load-side capacitor to swing the impedance
around through region F and then on to hit the 50W line in the -jX zone. The required
strategies for matching any impedance with various popular types
of ATU will be discussed in detail shortly. The network for region
D incidentally, indicates that an antenna presenting an
impedance in this zone may be used with a series loading coil.
This should not be surprising given that region D is associated
with electrically short antennas. Not shown on the diagram is the fact that a step-down transformer can be used to shift impedances A and B into region E, and impedances C and D into region F; i.e., for an antenna system, the input impedance of which varies widely with frequency, knowledge of the Z-plane region is helpful in determining when to use a transformer, or more particularly, when to substitute a 1:1 balun or unun for one of a different ratio. As mentioned previously, in the case of antennas for amateur radio use, the standard diagnostic for adjustment of the matching network is the SWR meter. This should be used in conjunction with an antenna current meter, or a field-strength meter, but in many cases is not. The problem with the SWR meter is that it can tell the operator when the point Z=50+j0 has been reached, but it gives no indication of how to do so. Also, in the absence of information about how much energy is being transmitted through the ATU, there is the very real possibility with some types of matching network, that nearly all of the transmitter output will be delivered inadvertently to the loss resistance of the ATU inductor. A straw poll of HF radio operators will reveal that most claim to have ATU adjustment strategies which work for them, but that no single procedure emerges as the best method. There is a very good reason for this, which can be identified from the preceding information; which is that the optimum adjustment strategy depends on the region of the Z-plane in which the load impedance lies. If we can determine the Z-plane region, we can immediately determine the adjustment which gives the most efficient route to the desired matching point. It should be obvious by now, that the ability to assign a load impedance to a region of the Z-plane will greatly assist the matching process. How to do so becomes clear when the electrical attributes of the six regions are tabulated thus: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The table and diagram above indicate that the Z-plane region
can be determined by the use of three detectors: 1) A Resistance bridge balanced to give a a null output when R=50W. 2) A Reactance bridge (i.e., a phase bridge) balanced to give a null output when jX=0. 3) A Conductance bridge balanced to give a null output when G=20mS. The chosen nulling values can of course be modified for target impedances other than 50+j0. The unambiguous maching procedure using null measurements of R, G and f was first proposed in 1973 by Mike Underhill (G3LHZ) and Peter Lewis of Mullard (Philips) research laboratories [9]. The required bridges can be constructed using substantially the same components as an SWR bridge; i.e., if an SWR meter is to be included in an ATU, the addition of a rotary switch and a centre-zero meter will permit the additional measurements to be made. A suitable instrument can also be made for insertion in the line between the transmitter and the ATU or antenna. This device we have called a "Match Meter". The original Match Meter is described in an appendix, and the subject of bridges is developed in chapter 6. |
|
5-11. The Match Meter. In the following sections we will show what happens in impedance space (i.e., in the Z-plane) when the various popular matching networks (antenna tuners) are adjusted. The adjustment operations will be discussed on the basis that they can be monitored, in most cases, using a 'Match Meter', i.e., an RF bridge which gives null measurements of R, jX, and G. The insights gained by understanding what is happening in impedance space will show how many of the common networks can be (simultaneously) simplified, made cheaper to build, made more foolproof, and made more efficient. The Match Meter assigns the antenna system input impedance to one of six regions of the Z-plane, as indicated in the diagram above. This assignment identifies the ATU adjustments which must be made in order to bring the impedance to 50+j0 using combinations of series and parallel reactance. Note that if the impedance lies on the boundary between two regions, it may be assigned to one or the other, or moved, depending on the matching network available. The type of information available from the Match Meter incidentally, is not quite the same as the information provided by an antenna analyser such as the MFJ259 or 269; and a Match meter is considerably more ergonomic in its intended application. In particular, if an antenna analyser is used, calculation is required in order to find where the load lies in relation to the 20mS constant conductance circle, and the analyser has a limited reactance range and does not give the sign of the reactance directly. Note that if an ATU has in integral balun, it does not matter from the Match Meter's point of view whether the balun is placed at the input side or the output side of the ATU. If a step-up or step-down balun is placed at the output (antenna) side of the ATU, it will simply scale the antenna system impedance to give a new impedance, and it is this scaled impedance which must be matched. If a step-up or step-down balun is placed at the input (transmitter) side of the ATU, it will scale all of the impedances seen by the match meter during the matching process, but it will also scale the target impedance, so making no difference to the operations involved. Consequently, any balun built into an ATU can be ignored for the purposes of analysing how the ATU works, but must be taken into account when determining the actual component values required.  |
© D W Knight 2007.
David Knight and Nigel Williams assert their right to be recognised as the authors of this work.
|
|
|
|
|
 |