Magnitude difference bridges, part 3. David Knight.

6.5 Magnitude-Difference Bridges. Part 3.

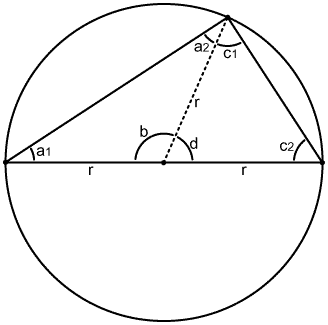
14.1. Circumscribed circle theorem.
14.2. Quadrature theorem.

15. Conductance bridges.
>>> Writing in progress!

14: Phasor theorems:
Knowledge of the following theorems is reqired for an understanding of conductance and phase bridges.

14.1. Circumscribed circle of a right-angled triangle:
The hypotenuse of a right-angled triangle lies on a diameter of the circumscribed circle.

Proof:
Consider a triangle constructed with its base on the diameter of a circle and its apex just touching the circle at an arbitrary point. This triangle can be divided into two isosceles triangles (i.e., triangles having two equal sides and two equal angles), the equal sides all being radii (radiuses, r) of the circle.
Using the definitions in the drawing, it follows that angles a1 and a2 are equal, and angles c1 and c2 are equal. We can therefore drop the subscripts (1 and 2) and use the notation: a=a1=a2 and c=c1=c2. Now, the three angles of a triangle add up to 180°. Therefore:

2a + b = 180°

and

2c + d = 180°

hence:

2a + b + 2c + d = 360°

but, by inspection;

b + d = 180°

hence:

2a + 2c = 180°

i.e.,

a + c = 90°

therefore:

a2 + c1 = 90°

14.2. Quadrature theorem: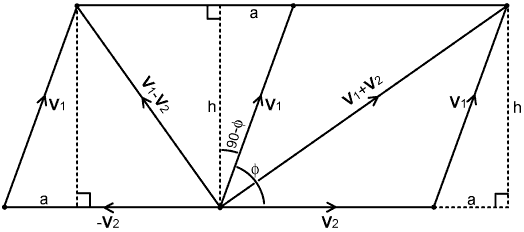
The magnitude of the sum of the two non-zero phasors is equal to the magnitude of their difference, if (and only if) the two phasors are in quadrature (i.e., when the angle between them is 90°).

Proof:
The diagram below shows two arbitrary phasors V1 and V2 with an arbitrary phase relationship φ.

Using the definitions given in the diagram, the magnitude of the sum of V1 and V2 is:

| V1 + V2 | = √ [ (|V2| + a)² + h² ]

and the magnitude of the difference is:

| V1 - V2 | = √ [ (-|V2| + a)² + h² ]

Now if

| V1 + V2 | = | V1 - V2 |

then

(|V2| + a)² + h² = (-|V2| + a)² + h²

(a + |V2|)² = (a -|V2|)²

a² +2a|V2| + |V2|² = a² -2a|V2| +|V2|²

hence:

a|V2| = -a|V2|

Which can only be true when a = 0 or V2 = 0.

Now, when a=0, Tan(90-φ)=a/h=0, and therefore φ=90°.
Thus if V1 and V2 are finite (non-zero): |V1+V2| = |V1-V2| only when φ=90°.

15. Conductance Bridges:
Recall that admittance is defined as:

Y = 1/Z = G + jB

Where G is conductance and B is susceptance. A pure reactance Xp (say), has a pure susceptance Bp = -1/Xp. When two admittances are placed in parallel, the new admittance is obtained by simple addition. Hence if an admittance jBp is placed in parallel with an admittance Y we get:

Y + jBp = G + j(B + Bp)

It follows, that when a pure reactance is placed in parallel with an impedance, conductance is unaffected. When the locus of an impedance (i.e., its point in the Z-plane) is constrained by the condition of constant conductance, its path in the Z-plane is a circle that has the two points 0+j0 and R+j0 on opposite ends of a diameter.
A conductance (G) transmission-bridge is a bridge that will remain balanced when an arbitrary (but non-zero) pure reactance is placed in parallel with the target load resistance. The utility of such an instrument lies in the fact that, if an operation is performed to move an impedance onto the constant conductance circle corresponding to G0 = 1/R0, then the impedance matching process can be completed by adjusting a reactance placed in parallel with the load.
Conductance is the reciprocal-space counterpart of resistance. Therefore the balance equation for a conductance bridge can be obtained by taking the equation for a resistance bridge and substituting Vv for Vi and vice versa. Looking at the problem formally however, we should start by defining Vv and Vi as admittance analogs, and so (with reference to Table 12.1) take Vv to represent G0 (assuming B0=0), and Vi to represent Y. We then specify that the bridge must balance when G=G0, i.e., Y=G0+jB, regardless of the value of B. Now we observe that:

G0 +jB -2G0 = -G0 +jB

has the same magnitude as G0+jB. The solution is therefore:

|Y - 2G0| = |Y| when G = G0

which, when replaced by its analogs gives:

| Vi -2Vv | = | Vi | when G = G0.

This balance relationship can be proved by considering the phasor relationships shown in the diagram below:

When R0 and Z lie on the same constant conductance circle in the Z-plane, Vv and Vi lie on a corresponding circle in the sample-voltage space. When that situation prevails, theorem 14.1 tells us that the phasors Vv and Vv-Vi are in quadrature. When two phasors are in quadrature, the magnitude of their sum is equal to the magnitude of their difference (theorem 14.2). Hence:
| Vv + Vv - Vi | = | Vv - ( Vv - Vi ) |
i.e.:
| 2Vv - Vi | = | Vi |

The corollary, of course, is that:

|2Vv-Vi| ≠ |Vi| when G ≠ G0

A phasor diagram corresponding to that situation is shown below:

Notice here that when Z is inside the G0 constant conductance circle, then G>G0, and vice versa. Conductance has a reciprocal relationship with impedance and so increases as the origin of the Z-plane (0+j0) is approached. Also notice the polarity information:

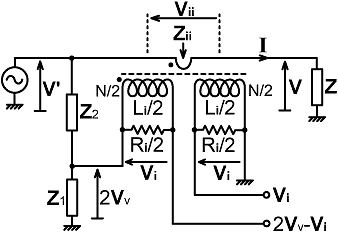
When |Vi| > |2Vv-Vi| , G > G0

It follows, that when the two rectified outputs of a conductance bridge are used to drive a centre-zero galvanometer, the +|Vi| output should be connected to the meter's (+) terminal.
A prototype bridge circuit is shown below. In this case, we define the output of the voltage-sampling network as 2Vv, and the outputs of both current-transformer secondary windings added together as 2Vi. Thus we have:

2Vi = I Zi / N = V Zi / (N Z)

where:

Zi = Rik // jXLi

(Rik being the effective secondary load after taking losses into account) and

2Vv = V' Z1 / (Z1 + Z2)

where:

V' = V + Vii = V [1 + Zii/Z]

i.e.:

V' = V [1 + Zi/(N² Z)]

As before, Vv=Vi when Z=R0; and so, due to the factor of 2 in both sample-voltage definitions, the network solution is the same as for a Z bridge; i.e.:

Zi / (N Z) = [1 + Zi/(N² Z)] Z1 / (Z1 + Z2)

Which can be rearranged to give:

N R0

- 1

When the bridge outputs are loaded, a port balancing network ( ZV = Z1//Z2 ) is needed in order to achieve optimum accuracy. The voltages obtained are shown in the diagram below:

For accurate DC port balancing, Z2 should be a DC open-circuit. Notice also that the ZV network has been placed on the earthed side of the winding used for the "Vi" output. It can go on either side in principle; but the capacitance of the Faraday-shield (if used) forms part of Z1, and so the arrangement shown gives best symmetry. The phasing of the "Vi" winding is, of course, irrelevant because |Vi| = |-Vi|. The two secondary windings should however be electrostatically isolated; i.e., they should not be in physical contact, and they should definitely not be wound as a bifilar pair.

.

>>>>>>>>

Writing in progress.

Citation:
Broad-band reflectometers at high-frequencies. R T Adams, Alexander Hovarth. Electrical Communication. 32(2), 1955. p118-125.
Resistive voltage sampling, resistive or transformer current sampling, 300KHz - 30MHz. Resistance, conductance and phase bridges are described.

>>>
Less severe loading defect because Ri << Rdet..

G bridge balances when Z = R0 // jX , regardless of X. It was shown in [A6.4] that balance error due to current transformer secondary parallel reactance is equivalent to a reactance of opposite sign in parallel with the load. Since the balance point of a G bridge is immune to such reactance, the bridge requires neither LF compensation nor HF neutralisation. If we use CVS however, LF comp resistor provides diode DC return (but there is no need to make it adjustable).

Amplitude balancing is required for accurate sysnthesis of the vector 2Vv-Vi.
.

>>>>

Phase bridges
-- Generic scheme (DBM), quadrature networks. Unloaded transformers. Transparent (broadband matched) phase bridge.

-- Poles and zeros. Diode limiter solution. Distortion? - put the TR relay after the bridge.

Combination bridges. - switching off current transformers by shorting Faraday shield.

Tapping the LF comp resistor for multi-function bridges

pros and cons of getting Vi/2 from the VS network or the summing network. Double diode rectifier.

TX to Ae

Ch.6 Contents

<< 6.5 Part 2