|
|
|
|
|
|
 Fig.
6-17#1
Fig.
6-17#1| Vi = I Ri / Ni |
|
| V = I (Zii + ZL) |
|
| Zii = Rii = Ri / Ni² |
|
| Vi = V Ri / [ Ni (Rii + ZL) ] |
| Vi = V Ri / [( Ri / Ni ) + Ni ZL] |
| ηi = Vi / V = Ri / [ Ni (Rii + ZL) ] |
| η0 = Ri / [ Ni (Rii + R0) ] |
| η0 = Ri / (Ni R0) |
| ηv = Vv / V = R1 / (R1 + R2) |
| η0 = Ri / [ Ni (Rii + R0) ] = R1 / (R1 + R2) |
|
R0 |
|
(R1 + R2) |
|
(Rii + R0) |
| R1 + R2 = R0 (Rii + R0) / Rii |
| Zbal = R0 (XLi² + j XLi Ri) / ( Ri² + XLi² ) |
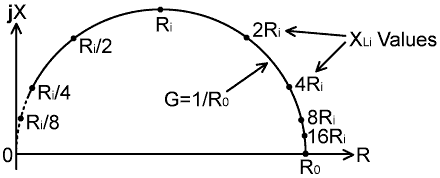 Fig.
6-18#1
Fig.
6-18#1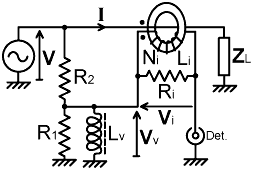 Fig.
6-18#3.
Fig.
6-18#3.| η0 = (jXLi // Ri) / Ni R0 |
| ηv = (R1 // jXLv // R2) / R2 |
| Ni R0 [ (1/jXLi) + (1/Ri) ] = R2 [ (1/R1) + (1/jXLv) + (1/R2) ] |
| Lv = Li R2 / Ni R0 |
 Fig.
6-18#4.
Fig.
6-18#4.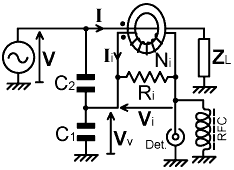
| ηv = Vv / V = C2 / (C1 + C2 ) |
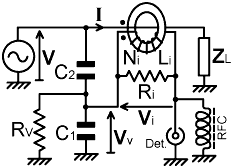
| 1/ηv = [ (C1 + C2) / C2 ] + 1/(j2πf C2 Rv ) |
| Rv = Li / Ni R0 C2 |
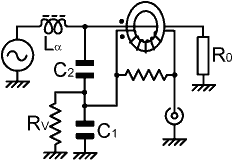
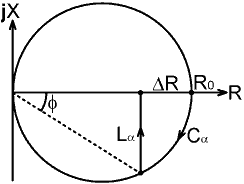
| Lα = Cα R0² gives zero generator phase angle at balance when XCα² >> R0² |
|
|
|
|
|