|
|
|
|
|
|
2. Components and Materials: Part 3.
Contents:
|
2-7. Resistor models. 2-8. Resistors and skin effect. |
2-9. Wirewound and helical resistors. 2-10. Resistor voltage ratings. |
|
2-7. Resistor models: The reader should be in no doubt by now that a resistor must be regarded as an impedance rather than as a pure resistance; and the issue we will tackle next is that of the high-frequency electrical behaviour of resistors. To quantify this, we must construct equivalent circuits involving resistance and reactance; and two possibilities are shown below: |
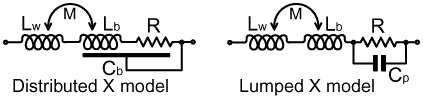
|
In both models, the resistor is shown to have a body inductance
Lb, and an actual or DC resistance R.
The body inductance is also shown to be linked to the external
circuit (or wiring) inductance Lw by a
magnetic interaction (or mutual inductance) M; this being
done as a reminder of the discussion in the previous section,
where we showed that these two inductances cannot be disentangled.
It is assumed in both cases that the resistance of the wires
is very small in comparison to the total resistance, and can
therefore be ignored; this being a reasonable assumption except
when dealing with resistors of very low value. In the distributed reactance model (above left), it is assumed that the resistance and the body inductance are intermingled, and that the body capacitance Cb is distributed over this composite object. This is a pretty accurate description of the resistor, but the mathematical analysis of such a model is necessarily complicated. We therefore revert to the simplified 'lumped reactance' model (above right); which is accurate enough for HF radio purposes; and with some reservations, up to VHF. In this case we have simply extracted the body inductance, and the capacitance is now represented as a shunt Cp (p stands for 'parallel' in this case) across the actual resistance R. Now, since we have opted for the approximation that the body capacitance is not associated with the body inductance, we can lump Lw with Lb to produce the standard resistor model shown below: |
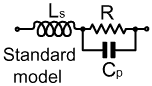 |
Ls = Lumped series inductance R = DC Resistance Cp = Lumped parallel capacitance. |
|
Notice that all of the resistor models seen so far are physically
realistic in the sense that if any of these hypothetical networks
is measured using DC, the result will be the actual resistance
R. In [AC Theory, Section 18], we noted that any impedance in parallel form can be converted into an impedance in series form. We can therefore convert the parallel combination of R and Cp into into a series combination of resistance and capacitance as shown below: |
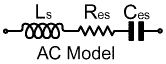 |
Ls = Series inductance Res = Equivalent Series Resistance (ESR) Ces = Series equivalent capacitance. |
|
The new resistance that results, Res,
is called the equivalent series resistance or ESR
of the device. It is not identical to, and can deviate substantially
from, the actual resistance. This AC-only model is not physically
realistic because it will not pass DC, but it allows us to represent
the impedance perfectly well; and since all of the elements are
now in series, we may reduce the impedance to the standard R+jX
form. We will now make use of the double-slash notation introduced in [AC Theory, Section 17], where ' // ' should be read as: "in parallel with". Using this notation, we can write the combination of the actual resistance R and its parallel capacitance Cp as an impedance without introducing new symbols, thus: R // jXCp = Res + jXCes The translation from the left-hand side to the right-hand side of this equation was given in [AC Theory, Section 18], and we can write it down using symbols appropriate to the present context as: |
|
|
( R² + XCp² ) |
|
|
( R² + XCp² ) |
|
Now notice in the left hand expression for Res;
that if XCp² is much greater than
R², then the bottom part of the fraction becomes approximately
equal to XCp² and so will cancel
the XCp² term in the top part. This
means that: only if XCp has a large magnitude
in relation to R, i.e., only if Cp is
very small (XCp=-1/2πfCp),
will the ESR (equivalent series resistance) Res
be close in value to the actual resistance R. This tells us immediately
that we cannot expect high-value resistors to behave well
at radio frequencies. A wire-ended ½Watt carbon-film resistor will typically have a shunt capacitance in the range 0.2 - 0.5 pF, and a metal film resistor typically 0.2 - 0.6 pF [20]. This value depends on the insulating materials used in the construction of the resistor, and will vary from manufacturer to manufacturer. The series inductance can be estimated using the techniques given in the previous section, and we will base our investigation on the assumption that, for a wire-ended ½ Watt resistor with reasonably short leads, it will be about 14 nH. We can use these pieces of information to show how the impedance of a particular type of resistor might vary in relation to the nominal (DC) resistance value. Here we will do so on the pessimistic assumption that the capacitance of an un-documented (i.e., cheap) resistor will be at the high-end of the typical range. The model we will explore is shown below (the symbol ' ≡ ' means "is equivalent to"): |
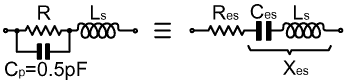
|
The quantities involved in the calculation are: XLs = 2πf Ls, where Ls = 14 nH (in this example) XCp = -1/(2πf Cp), where Cp = 0.5 pF XCes = XCp R² / ( R² + XCp² ) Res = R XCp² / ( R² + XCp² ) Xes = XLs + XCes The impedance of the resistor is: Z = Res + jXes but, since the inductance is somewhat variable depending on the magnetic environment, we will use the alternative definition: Z = ( R // jXCp ) + jXLs This allows us to treat the circuit inductance as a separate element, so that we may determine the conditions under which it should be considered to be important. The results for some spot frequencies are tabulated below, first for (R//jXCp)=Res+jXCes and then for XLs. To obtain the actual impedance at a particular frequency, add the reactance in the second table to the imaginary part of the impedance in the first table. All calculations were performed using a spreadsheet program. |
Impedance / Ω of a pure resistance in parallel with 0.5 pF.
|
|
||||||
|
|
|
|
|
|
|
|
|
|
-j0.031 |
-j0.099 |
-j0.314 |
-j0.993 |
-j3.138 |
-j9.837 |
|
|
-j3.142 |
-j9.934 |
-j31.385 |
-j98.375 |
-j285.938 |
-j499.989 |
|
|
-j313.85 |
-j983.75 |
-j2859.38 |
-j4999.89 |
-j2890.26 |
-j996.49 |
|
|
-j28593.8 |
-j49998.9 |
-j28902.5 |
-j9964.9 |
-j3179.9 |
-j1006.5 |
|
|
-j289025.5 |
-j99648.8 |
-j31798.8 |
-j10064.8 |
-j3183.1 |
-j1006.6 |
Reactance / Ω of a 14 nH series inductance
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The impedances appearing in the table tell us that a 100 Ω
resistor is very nearly a perfect component over the entire HF
spectrum, and a 1 kΩ resistor is not too bad. Our cheap
10 kΩ resistor however, has an impedance of about 5000-j5000
Ω at 32 MHz, and resistors of higher value than that are
basically just poor-quality capacitors. This does not mean that
high value resistors are of no use at radio frequencies; a 1
MΩ resistor providing DC bias to the gate of a JFET, for
example, will still do its job, but from a radio-frequency point
of view, it simply adds about 0.5 pF of stray capacitance to
the amplifier input impedance. With regard to the series inductance, notice that only the 100 Ω resistor (in this set of examples) is capable of displaying a positive reactance when the inductive reactance is added. In all other instances, the impedance is vastly dominated by the capacitance, and the circuit inductance is effectively immaterial. Finally, to drive home the point, more comprehensive calculations for the real part of the resistor impedance (the ESR) are shown in the graph below. |
|
(pure resistance in parallel with 0.5 pF) |

| The only qualification we should give to these calculations is that they are somewhat more pessimistic than the graphs for typical resistors given in reference [20], i.e., better characteristics can be obtained by specifying resistors with low self-capacitance; but for those who do not have access to a network analyser or a universal bridge, the behaviour of resistors of unknown origin must be assumed to be that of the worst case. Note also that these calculations represent performance considerably better than can be expected from carbon slug (composition) resistors [21]. |
| In the vast majority of radio applications, the high-frequency behaviour of resistors is not a problem, because all the resistor is required to do is inject DC into some part of a circuit to make the transistors work. The actual impedance is not important, because RF circuits are usually designed in such a way that the reactive component will be swamped by or absorbed into some other other circuit reactance (such as a decoupling capacitor). Problems are likely to arise however when resistors are used to construct supposedly accurate RF voltage-divider networks. Such a network is shown on the right, with the low-frequency (i.e., DC) equation for the output voltage below it. We know, of course, that the complete expression for the output voltage is: |
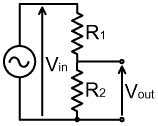
|
|
Vout = Vin
Z2 / ( Z1
+ Z2) and that, in general, the output voltage will be complex; i.e., it will not be exactly in phase with the input voltage. The simple resistive voltage divider often appears in amateur SWR bridge designs, where it is used to sample the voltage output from the radio transmitter. The output voltage of the network sets the balance-point of the bridge; i.e., it dictates the transmitter load impedance for which the bridge reads 1:1 SWR. We now know that if resistors of much greater than 1 kΩ are used in the network, the output voltage may have serious errors in both magnitude and phase at the high-end of the HF spectrum. The problem however, is that low-value resistors will absorb significant power from the transmitter and generate considerable heat; and people like to leave SWR bridges in situ during transmitter operation. There are consequently bridges in existence that use values for R1 in the 5 k to 15 kΩ range, and we must have profound doubts about the accuracy of such instruments. If a voltage sampling network working at radio frequencies is required to have a high input impedance, some form of compensation scheme, or the use of a capacitive potential divider or a transformer, is indicated. This subject is explored in detail in chapter 6. We should also comment, at this point, on the old practice of connecting several resistors in parallel to make a dummy-load resistor. This idea is based in the presumption that resistors are inductive. Since resistors of greater than about 100 Ω are likely to be capacitive, and low-value resistors give better performance at radio frequencies than high value-resistors; the practice of connecting several high-value resistors in parallel in order to obtain a low-value resistor will probably not achieve the desired effect. The sensible way to make a dummy-load is to use a single low-capacitance resistor, of the appropriate power rating. Low capacitance construction in cylindrical resistors, incidentally, involves making the resistor in the form of a hollow tube; the reason being that the capacitance is dictated by the dielectric constant of the resistor substrate, and air has a much lower dielectric constant than any solid material. Dielectrics are discussed later in this chapter. This investigation incidentally, tells us something of general significance, which is that: if a physically realistic model for a device requires a pure resistance in parallel with a reactance, the apparent resistance of that device must vary with frequency. If the dominant parallel element is capacitive, as it is in the case of a carbon or metal-film resistor, the effective resistance will fall with frequency. If the dominant parallel element is inductive, as it is in the case of a wire or low-resistance conductor, the effective resistance will increase with frequency. |
|
2-8. Resistors and skin effect: Equation (2-2.2), the expression for skin-depth given earlier, may be rewritten:
|

| 50 Ω dummy-load resistor and shielding tube (Assemby from a 1960s Redifon HF aviation transmitter. Resistor manufactured by Electrosil). The resistor is constructed as a thin film deposited on to a glass tube, with silvered contacts and a coat of protective paint. |
|
The reader might, of course, be inclined to wonder; if the ESR
(equivalent series resistance) of carbon and metal-film resistors
falls with frequency due to parallel capacitance, and the resistance
of conductors rises with frequency, then why are resistors not
constructed in such a way as to maximise the skin effect.
The answer is that the skin effect, being described by a square-root
frequency law, causes an initial rapid rise in resistance that
tails off as the frequency increases; whereas parallel capacitance
barely affects the resistor ESR at low frequencies, but causes
it to plummet over the course of a decade or so once a certain
turnover frequency has been reached. These two types of
behaviour are definitely not complementary, and so it is better
to optimise the performance of a resistor below its turnover
frequency by minimising the skin effect. One final comment on the subject of metal-film resistors, which deserves a place in the annals of bad physics, was found (once again) in the Hi-Fi literature. The author in question, a 'golden-eared' reviewer of audio equipment, asserted that amplifiers that use metal-film resistors have a "metallic sound"; which, as he helpfully explained, is because such resistors, consisting only of a thin layer of metal, suffer from something called the 'skin effect'. 2-9. Wirewound and helical resistors: Most readers will be aware that wirewound resistors are highly inductive, and are therefore generally unsuitable for RF signal-path applications (unless the resistor is also required to function as a low-Q inductor). Bob Botos of Hewlett-Packard gives the typical inductance ranges for general-purpose wirewound resistors in reference [20], these being 0.03 to 2.5 μH for ¼ W, 0.2 to 33 μH for ½ W, and 0.4 to 56 μH for 2 to 4 W sizes. The high end of the inductance range is associated with high resistance values, for the simple reason that high-value resistors require the greatest length of resistance wire and consequently have more turns. Wirewound resistors therefore, must never be used to terminate transmission lines or construct RF attenuators and voltage dividers. What should be noted in addition however, is that some types of metal and metal-oxide resistors are also inductive; the reason being that they have a helix etched-out of the resistive film in order to increase the length of the conducting track and reduce its cross-sectional area. Such inductive construction is seen (for example) in older high-precision resistors intended for DC or low-frequency applications, and the helical groove can often (but not always) be seen through the protective paint. Helical construction is also seen in very high-value resistors (tens of MΩ), but in that case we already know that such devices do not function as resistors at high frequencies. |
 Helical film resistors |
|
Bifilar winding |
|
Some readers will also be aware that there is such a thing
as a "non-inductive" wirewound resistor. This type
of resistor can be constructed by taking a length of resistance
wire, folding it in the middle, and winding it around a ceramic
cylinder; the resulting topology being known as bi-filar
winding (see illustration, above right). In this way, two closely-coupled
coils are produced, and the magnetic interaction is such that
the inductance of one is cancelled by the inductance of the other.
Unfortunately, this type of resistor is still unsuitable for
RF applications, for various reasons: Firstly, the inductance
cancellation will not be complete because the magnetic coupling
between the two coils will not be perfect. To use the language
of transformer theory; there will be some leakage inductance.
Secondly, although resistance-wire alloys (Constantan ρ=490
nΩm, and Manganin ρ=440 nΩm) have relatively
high resistivities, the radius of the wire may still be greater
than the skin-depth at some frequencies, particularly for the
lower value resistors that use thicker wire. Thirdly, the length
of wire used may be an appreciable fraction of a wavelength at
radio frequencies, in which case the resistor will behave as
a short-circuited transmission-line, and although the wave reflected
from the far-end of the resistor will tend to be absorbed by
the resistive material, it will still cause the impedance seen
at the resistor terminals to vary with frequency. Finally, the
RF resistance of the device is subject to the vagaries of the
proximity effect, exacerbated by the need for tight inductive
coupling between the windings. Other non-inductive winding methods
are described in refs [20]
and [24], but all are subject
to similar objections. |
© D W Knight 2007, 2014.
David Knight asserts the right to be recognised as the author of this work.
|
|
|
|
|
|
u
